Problem Statement:
Write a program to implement matrix multiplication using Strassen's method. (Divide and
Conquer).
Theory:
Strassen's method:
Following is simple Divide and Conquer
method to multiply two square matrices.
1) Divide matrices A and B in 4 sub-matrices of
size N/2 x N/2 as shown in the below diagram.
2) Calculate following values recursively. ae +
bg, af + bh, ce + dg and cf + dh
In the above method, we do 8 multiplications for matrices of size
N/2 x N/2 and 4 additions. Addition of two matrices takes O(N2)
time. So the time complexity can be written as
T(N) = 8T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is O(N3)
which is unfortunately same as the above naïve method.
Simple Divide
and Conquer also leads to O(N3), can there be a better way?
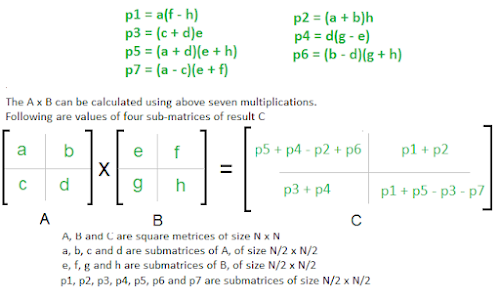
In the above divide and conquer method, the main component for high time
complexity is 8 recursive calls. The idea of Strassen’s method is to reduce the number of recursive
calls to 7. Strassen’s method is similar to above simple divide and conquer
method in the sense that this method also divide matrices to sub-matrices of
size N/2 x N/2 as shown in the above diagram, but in Strassen’s method, the
four sub-matrices of result are calculated using following formulae.
Time Complexity of Strassen’s Method
Addition and Subtraction of two matrices takes O(N2) time. So time
complexity can be written as
T(N) = 7T(N/2) + O(N2)
From Master's Theorem, time complexity of above method is
O(NLog7) which is approximately O(N2.8074)
Generally Strassen’s Method is not preferred for practical
applications for following reasons.
1) The constants used in Strassen’s method are high and for a typical
application Naive method works better.
2) For Sparse matrices, there are better methods especially designed for them.
3) The submatrices in recursion take extra space.
4) Because of the limited precision of computer arithmetic on noninteger
values, larger errors accumulate in Strassen’s algorithm than in Naive Method
Code in C++
#include<iostream>
using namespace std;
int** Add_matrix(int**A,int** B,int n)
{
int **C=new int*[n];
for(int i=0;i<n;i++){
C[i]=new int[n];
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
C[i][j]=A[i][j]+B[i][j];
}
}
return C;
}
int** Sub_matrix(int **A,int **B,int n)
{
int **C=new int*[n];
for(int i=0;i<n;i++){
C[i]=new int[n];
}
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
C[i][j]=A[i][j]-B[i][j];
}
}
return C;
}
void input_Matrix(int **A, int n)
{
cout<<"\n";
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<"\t Enter ["<<i<<"]["<<j<<"] = ";
cin>>A[i][j];
}
}
}
void display_Matrix(int **A, int n)
{
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout<<"\t"<<A[i][j];
}
cout<<endl;
}
}
int **MM_S_DC(int **A,int **B,int n)
{
if(n==2)
{
int** C= new int*[n];
for(int i=0;i<n;i++){
C[i]=new int[n];
}
int p1,p2,p3,p4,p5,p6,p7;
p1=(A[0][0]+A[1][1])*(B[0][0]+B[1][1]);
p2=(A[1][0]+A[1][1])* B[0][0];
p3=(B[0][1]-B[1][1])* A[0][0];
p4= (B[1][0]-B[0][0])*A[1][1];
p5= (A[0][0]+A[0][1])* B[1][1];
p6= (A[1][0]-A[0][0])*(B[0][0]+B[0][1]);
p7=(A[0][1]-A[1][1])*(B[1][0]+B[1][1]);
C[0][0]=p1+p4-p5+p7;
C[0][1]=p3+p5;
C[1][0]=p2+p4;
C[1][1]=p1+p3-p2+p6;
return C;
}
else{
int** A11= new int*[n/2];
int** A12= new int*[n/2];
int** A21= new int*[n/2];
int** A22= new int*[n/2];
int** B11= new int*[n/2];
int** B12= new int*[n/2];
int** B21= new int*[n/2];
int** B22= new int*[n/2];
int** C11= new int*[n/2];
int** C12= new int*[n/2];
int** C21= new int*[n/2];
int** C22= new int*[n/2];
int** P1=new int*[n/2];
int** P2=new int*[n/2];
int** P3=new int*[n/2];
int** P4=new int*[n/2];
int** P5=new int*[n/2];
int** P6=new int*[n/2];
int** P7=new int*[n/2];
int** C=new int*[n];
for(int i=0;i<n;i++){
C[i]=new int[n];
}
for(int i=0;i<n/2;i++){
A11[i]=new int[n/2];
A12[i]=new int[n/2];
A21[i]=new int[n/2];
A22[i]=new int[n/2];
B11[i]=new int[n/2];
B12[i]=new int[n/2];
B21[i]=new int[n/2];
B22[i]=new int[n/2];
C11[i]=new int[n/2];
C12[i]=new int[n/2];
C21[i]=new int[n/2];
C22[i]=new int[n/2];
P1[i]=new int[n/2];
P2[i]=new int[n/2];
P3[i]=new int[n/2];
P4[i]=new int[n/2];
P5[i]=new int[n/2];
P6[i]=new int[n/2];
P7[i]=new int[n/2];
}
for(int i=0;i<n/2;i++)
{
for(int j=0;j<n/2;j++)
{
A11[i][j]=A[i][j];
A12[i][j]=A[i][j+n/2];
A21[i][j]=A[i+n/2][j];
A22[i][j]=A[i+n/2][j+n/2];
B11[i][j]=B[i][j];
B12[i][j]=B[i][j+n/2];
B21[i][j]=B[i+n/2][j];
B22[i][j]=B[i+n/2][j+n/2];
}
}
P1= MM_S_DC(Add_matrix(A11,A22,n/2),Add_matrix(B11,B22,n/2),n/2);//P1 = (A00 + A11 ) * (B00 + B11)
P2= MM_S_DC(Add_matrix(A21,A22,n/2),B11,n/2); //P2 = (A10 + A11 ) * B00;
P3= MM_S_DC(Sub_matrix(B12,B22,n/2),A11,n/2); //P3= (BO1 - B11 ) * A00;
P4= MM_S_DC(A22,Sub_matrix(B21,B11,n/2),n/2); //P4 = (B10 - B00 ) * A11;
P5= MM_S_DC(Add_matrix(A11,A12,n/2),B22,n/2); //P5 = (A00 + A01 ) * B11;
P6= MM_S_DC(Sub_matrix(A21,A11,n/2),Add_matrix(B11,B12,n/2),n/2);//P6 = (A10 + A00 ) * (B00 + B01)
P7= MM_S_DC(Sub_matrix(A12,A22,n/2),Add_matrix(B21,B22,n/2),n/2);//P7 = (A01 - A11 ) * (B10 + B11);
C11= Add_matrix(P1,Add_matrix(P4,Sub_matrix(P7,P5,n/2),n/2),n/2);//C1= P1 + P4 - P5 + P7
C12= Add_matrix(P4,P5,n/2); //C2= P3 + P5
C21= Add_matrix(P2,P4,n/2); //C3= P2 +P4
C22= Add_matrix(P1,Add_matrix(P3,Sub_matrix(P6,P2,n/2),n/2),n/2);//C4 = P1 + P3 - P2 + P6
for(int i=0;i<n/2;i++)
{
for(int j=0;j<n/2;j++)
{
C[i][j]= C11[i][j];
C[i][j+n/2]=C12[i][j];
C[i+n/2][j]=C21[i][j];
C[i+n/2][j+n/2]=C22[i][j];
}
}
return C;
}
}
int main()
{
int **A, **B, **C, n;
cout<<"==========Matrix Multiplication using MM_S_DC's Method(Divide and Conquer) \n";
cout<<"\n \t Enter the n of matrix: \n";
cin>>n;
A = new int*[n];
B = new int*[n];
C = new int*[n];
for(int i=0; i<n;i++){
A[i] = new int[n];
B[i] = new int[n];
C[i] = new int[n];
}
cout<<"\n\t Enter the First Matrix";
input_Matrix(A,n);
cout<<"\n\t Enter the Second Matrix";
input_Matrix(B,n);
cout<<"\n\t First Matrix = \n";
display_Matrix(A,n);
cout<<"\n\t Second Matrix = \n";
display_Matrix(B,n);
C = MM_S_DC(A,B,n);
cout<<"\nMultiplication of both matrix is \n";
display_Matrix(C,n);
return 0;
}
OUTPUT




Comments
Post a Comment