Assignment 6: Write a recursive program to find the solution of placing n queens on chess board so that no queen takes each other (backtracking).

Problem Statement: Write a recursive program to find the solution of placing n queens on chess board so that no queen takes each other (backtracking).

Theory: 

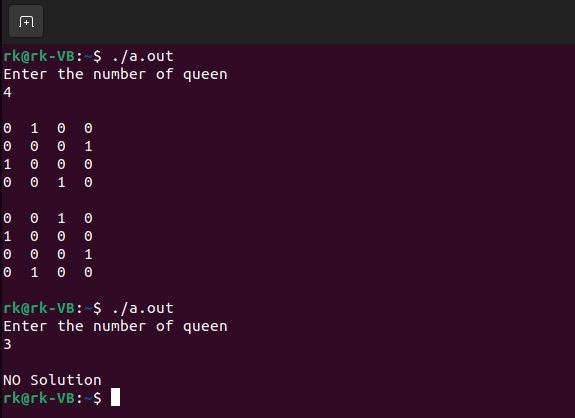
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, following is a solution for 4 Queen problem.

The expected output is a binary matrix which has 1s for the blocks where queens are placed. For example, following is the output matrix for above 4 queen solution.  

              { 0,  1,  0,  0}

              { 0,  0,  0,  1}

              { 1,  0,  0,  0}

              { 0,  0,  1,  0}

Naive Algorithm

Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints. 

while there are untried configurations

{

   generate the next configuration

   if queens don't attack in this configuration then

   {

     print this configuration;

   }

} 

Backtracking Algorithm
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.

bool IsBoardOk (chessboard, row R, column C) {
     If there is a queen ‘Q’ positioned to the left of column C in row R, then
         return False;
     If there is queen ‘Q’ positioned on the upper left diagonal, then
         return false;
     If there is queen ‘Q’ positioned on the lower left diagonal, then
         return false;
     return true;
}
PlaceNQueens ( chessboard, column )
a) If the chessboard size equals column number (chessboard.size() == column)
    All the queens are correctly placed on the chessboard. Display the chessboard.

b) Else try placing the queen on each row of the column and check if the chessboard remains valid.
    for ( row = 0; row < chessboard.size(); row++ )
        Place the queen ‘Q’ at position [ row, column ] and check if the chessboard remains valid
        chessboard [ row ] [ column ] = ' Q ‘
        Check if ( IsBoardOk ( chessboard, row, column ) == true ) {
            Try placing another queen ‘Q’ in the next column.
            PlaceNQueens ( chessboard, column + 1 ) ;
        }
        Chessboard was not valid hence revert

        chessboard [ row ] [ column ] = ' . ‘.

Time complexity of N queens algorithm : For finding a single solution where the first queen ‘Q’ has been assigned the first column and can be put on N positions, the second queen has been assigned the second column and would choose from N-1 possible positions and so on; the time complexity is O ( N ) * ( N - 1 ) * ( N - 2 ) * … 1 ). i.e The worst-case time complexity is O ( N! ). Thus, for finding all the solutions to the N Queens problem the time complexity runs in polynomial time.

Code

#include<iostream>

using namespace std;

int board[10][10];

void printboard(int n){

for(int i=0;i<n;i++){

cout<<endl;

for(int j=0;j<n;j++){

cout<< board[i][j] <<"  ";

}

}

cout<<endl;

}

bool isSafe(int col,int row, int n){

for(int i=0;i<row;i++){ //column

if(board[i][col]){

return false;

}

}

for(int i=row, j=col;i>=0 && j>=0; i--,j--){ //left diagonal

if(board[i][j]){

return false;

}

}

for(int i=row, j=col;i>=0 && j<n; i--,j++){ //right diagonal

if(board[i][j]){

return false;

}

}

return true;

}

bool NQsolve(int n, int row){

if(n == row){

printboard(n);

return true;

}

bool res = false;

for(int i=0;i<=n-1;i++){

if(isSafe(i,row,n)){

board[row][i] = 1;

res = NQsolve(n,row+1) || res;

board[row][i] = 0;

}

}

return res;

}

int main(){

int n;

cout<<"Enter the number of queen \n";

cin>>n;

for(int i=0;i<n;i++){

for(int j=0;j<n;j++){

board[i][j] = 0;

}

}

bool res = NQsolve(n, 0);

if(res == false){

cout<<"\nNO Solution \n";

}

else{

cout<<endl;

}

return 0;

}

Output